Generality in solutions; an example in HttpFile
A few (ok, ok, over a dozen) years ago, I came across a question by someone on stackoverflow who wanted to be able to unzip part of a ZIP file that was hosted on the web without having to download the entire file.
He had not found a Python library for doing this, so he modified the ZipFile library to create an HTTPZipFile class which knew about both ZIP files and also about HTTP requests. I posted a different approach. Over time, stackoverflow changed its goals and now that question and answer have been closed and marked off-topic for stackoverflow. I believe there's value in the question and answer, and I think a fuller treatment of the answer would be fruitful for others to learn from.
Seams and Layers
The idea is to think about the interfaces: the seams or layers in the code.
The ZipFile class expects a file object. The file in this case lives on a website, but we could create a file-like object that knows how to retrieve parts of a file over HTTP using Range GET requests, and behaves like a file in terms of being seekable.
Let's walk through this pedagogically:
We want to create a file-like object that takes a URL as its constructor.
So let's start with our demo script:
#!/usr/bin/env python3
from httpfile import HttpFile
# Try it
from zipfile import ZipFile
URL = "https://www.python.org/ftp/python/3.12.0/python-3.12.0-embed-amd64.zip"
my_zip = ZipFile(HttpFile(URL))
print("\n".join(my_zip.namelist()))
And create httpfile.py with just the constructor as a starting point:
#!/usr/bin/env python3
class HttpFile:
def __init__(self, url):
self.url = url
Trying that, we get:
AttributeError: 'HttpFile' object has no attribute 'seek'
So let's implement seek:
#!/usr/bin/env python3
import requests
class HttpFile:
def __init__(self, url):
self.url = url
self.offset = 0
self._size = -1
def size(self):
if self._size < 0:
response = requests.get(self.url, stream=True)
response.raise_for_status()
if response.status_code != 200:
raise OSError(f"Bad response of {response.status_code}")
self._size = int(response.headers["Content-length"], 10)
return self._size
def seek(self, offset, whence=0):
if whence == 0:
self.offset = offset
elif whence == 1:
self.offset += offset
elif whence == 2:
self.offset = self.size() + offset
else:
raise ValueError(f"whence value {whence} unsupported")
return self.offset
That gets us to the next error:
AttributeError: 'HttpFile' object has no attribute 'tell'
So we implement tell():
def tell(self):
return self.offset
Making progress, we reach the next error:
AttributeError: 'HttpFile' object has no attribute 'read'
So we implement read:
def read(self, count=-1):
if count < 0:
end = self.size() - 1
else:
end = self.offset + count - 1
headers = {
'Range': "bytes=%s-%s" % (self.offset, end),
}
response = requests.get(self.url, headers=headers, stream=True)
if response.status_code != 206:
raise OSError(f"Bad response of {response.status_code}")
# The headers contain the information we need to check that; in particular,
# When the server accepts the range request, we get
# Accept-Ranges: bytes
# Content-Length: 22
# Content-Range: bytes 27382-27403/27404
# vs when it does not accept the range:
# Content-Length: 27404
content_range = response.headers.get('Content-Range')
if not content_range:
raise OSError("Server does not support Range")
if content_range != f"bytes {self.offset}-{end}/{self.size()}":
raise OSError(f"Server returned unexpected range {content_range}")
# End of paranoia checks
chunk = len(response.content)
if count >= 0 and chunk != count:
raise OSError(f"Asked for {count} bytes but got {chunk}")
self.offset += chunk
return response.content
We have a lot going on here; particularly around handling error checking and ensuring the responses match what we expect. We want to fail loudly if we get something unexpected rather than attempt to forge ahead and fail in an obscure way later on.
And now we finally reach some success, giving a listing of the filenames within the ZIP:
python.exe pythonw.exe python312.dll python3.dll vcruntime140.dll vcruntime140_1.dll LICENSE.txt pyexpat.pyd select.pyd unicodedata.pyd winsound.pyd _asyncio.pyd _bz2.pyd _ctypes.pyd _decimal.pyd _elementtree.pyd _hashlib.pyd _lzma.pyd _msi.pyd _multiprocessing.pyd _overlapped.pyd _queue.pyd _socket.pyd _sqlite3.pyd _ssl.pyd _uuid.pyd _wmi.pyd _zoneinfo.pyd libcrypto-3.dll libffi-8.dll libssl-3.dll sqlite3.dll python312.zip python312._pth python.cat
So let's see if we can extract part of the LICENSE.txt file from within the zip:
data = my_zip.open('LICENSE.txt')
data.seek(99)
print(data.read(239).decode('utf-8'))
That triggers a new error (which a comment 8 years after the initial code was posted pointed out was needed as of Python 3.7):
AttributeError: 'HttpFile' object has no attribute 'seekable'
So a trivial implementation of that:
def seekable(self):
return True
and we now get the content:
Guido van Rossum at Stichting Mathematisch Centrum (CWI, see https://www.cwi.nl) in the Netherlands as a successor of a language called ABC. Guido remains Python's principal author, although it includes many contributions from others.
There are a number of ways to further improve this code for production use, but for our pedagogical purposes here, I think we can call that "good enough". (Areas of improvement from an engineering perspective include: actual unit tests, integration tests that do not rely on a remote server, filling out the file object's full interface, addressing the read-only nature of the file access, using a session to support authentication mechanisms and connection reuse, among others.)
This gets us an object that acts like a local file even though it's reaching over the network. The implementation requires less code than a modified HttpZipFile would.
This same interface of a file-like object can be used for other purposes as well.
A Second Application Of The Pattern
Let's continue with our motivating use case of accessing parts of remote zip files where we don't want to download the entire file. If we don't want to download the entire file, then surely we would not want to download part of the file multiple times, right? So we would like HttpFile to cache data. But then we wind up mixing caching into the HTTP logic. Instead, we can again use the file-like-object interface to add a caching layer for a file-like object.
So we will need a class that takes a file object and a location to save the cached data. To keep this simple, let's say we point to a directory where the cache for this one file object will be stored. We will want to be able to store the file's total size, every chunk of data, and where each chunk of data maps into the file. So let's say the directory can contain a file named size with the file's size as a base 10 string with a newline, and any number of data.<offset> files with a chunk of data. This makes it easy for a human to understand how the data on disk works. I would not call it exactly "self describing", but it does lean in that general direction. (There are many, many ways we could store the data in the cache directory. Each one has its own set of trade-offs. Here I'm aiming for ease of implementation and obviousness.)
Since the file's data will be stored in segments, we will want to be able to think in terms of segments which can be ordered, check if two segments overlap, or if one segment contains another. So let's create a class to provide that abstraction:
import functools
@functools.total_ordering
class Segment(object):
def __init__(self, offset, length):
self.offset = offset
self.length = length
def overlaps(self, other):
return (
self.offset < other.offset+other.length and
other.offset < self.offset + self.length
)
def contains(self, offset):
return self.offset <= offset < (self.offset + self.length)
def __lt__(self, other):
return (self.offset, self.length) < (other.offset, other.length)
def __eq__(self, other):
return self.offset == other.offset and self.length == other.length
Using that class, we can create a constructor that loads the metadata from the cache directory:
class CachingFile:
def __init__(self, fileobj, backingstore):
"""fileobj is a file-like object to cache. backingstore is a directory name.
"""
self.fileobj = fileobj
self.backingstore = backingstore
self.offset = 0
os.makedirs(backingstore, exist_ok=True)
try:
with open(os.path.join(backingstore, 'size'), 'r', encoding='utf-8') as size_file:
self._size = int(size_file.read().strip(), 10)
except Exception:
self._size = -1
# Get files and sizes for any pre-existing data, so
# self.available_segments is a sorted list of Segments.
self.available_segments = [
Segment(int(filename[len("data."):], 10), os.stat(os.path.join(self.backingstore, filename)).st_size)
for filename in os.listdir(self.backingstore) if filename.startswith("data.")]
and the simple seek/tell/seekable parts of the interface we learned above:
def size(self):
if self._size < 0:
self._size = self.fileobj.seek(0, 2)
with open(os.path.join(self.backingstore, 'size'), 'w', encoding='utf-8') as size_file:
size_file.write(f"{self._size}\n")
return self._size
def seek(self, offset, whence=0):
if whence == 0:
self.offset = offset
elif whence == 1:
self.offset += offset
elif whence == 2:
self.offset = self.size() + offset
else:
raise ValueError("Invalid whence")
return self.offset
def tell(self):
return self.offset
def seekable(self):
return True
Implementation of read() is a bit more complex. It needs to handle reads with nothing in the cache, reads with everything in the cache, but also reads with multiple cached and uncached segments.
def _read(self, offset, count):
"""Does not update self.offset"""
if offset >= self.size() or count == 0:
return b""
desired_segment = Segment(offset, count)
# Is there a cached segment for the start of this segment?
matches = sorted(segment for segment in self.available_segments if segment.contains(offset))
if matches: # Read data from cache
match = matches[0]
with open(os.path.join(self.backingstore, f"data.{match.offset}"), 'rb') as data_file:
data_file.seek( offset - match.offset )
data = data_file.read(min(offset+count, match.offset+match.length) - offset)
else: # Read data from underlying file
# The beginning of the requested data is not cached, but if a later
# portion of the data is cached, we don't want to re-read it, so
# request only up to the next cached segment..
matches = sorted(segment for segment in self.available_segments if segment.overlaps(desired_segment))
if matches:
match = matches[0]
chunk_size = match.offset - offset
else:
chunk_size = count
# Read from the underlying file object
if not self.fileobj:
raise RuntimeError(f"No underlying file to satisfy read of {count} bytes at offset {offset}")
self.fileobj.seek(offset)
data = self.fileobj.read(chunk_size)
# Save to the backing store
with open(os.path.join(self.backingstore, f"data.{offset}"), 'wb') as data_file:
data_file.write(data)
# Add it to the list of available segments
self.available_segments.append(Segment(offset, chunk_size))
# Read the rest of the data if needed
if len(data) < count:
data += self._read(offset+len(data), count-len(data))
return data
def read(self, count=-1):
if count < 0:
count = self.size() - self.offset
data = self._read(self.offset, count)
self.offset += len(data)
return data
Notice the RuntimeError raised if we created the CachingFile object with fileobj=None. Why would we ever do that? Well, if we have fully cached the file, then we can run entirely from cache. If the original file (or URL, in our HttpFile case) is no longer available, the cache may be all we have. Or perhaps we want to isolate some operation, so we run once in "non-isolated" mode with the file object passed in, and then run in "isolated" mode with no file object. If the second run works, we know we have locally cached everything needed for the operation in question.
Our motivation is to use this with HttpFile, but it could be used in other situations. Perhaps you have mounted an sshfs file system over a slow or expensive link; CachingFile would improve performance or reduce cost. Or maybe you have the original files on a harddrive, but put the cache on an SSD so repeated reads are faster. (Though in the latter case, Linux offers functionality that would likely be superior to anything implemented in Python.)
Generalized Lesson
So those are a couple of handy utilities, but they demonstrate a more profound point.
When you design your code around standard interfaces, your solutions can be applied in a broader range of situations, and reduce the amount of code you must write to achieve your goal.
When faced with a problem of the form "I want to perform an operation on <something>, but I only know how to operate on <something else>", consider if you can create code that takes the "something" you have, and provides an interface that looks like the "something else" that you can use. If you can write that code to adapt one kind of thing to another kind of thing, you can solve your problem without having to reimplement the operation you already have code to do. And you might find there are more uses for the result than you anticipated.
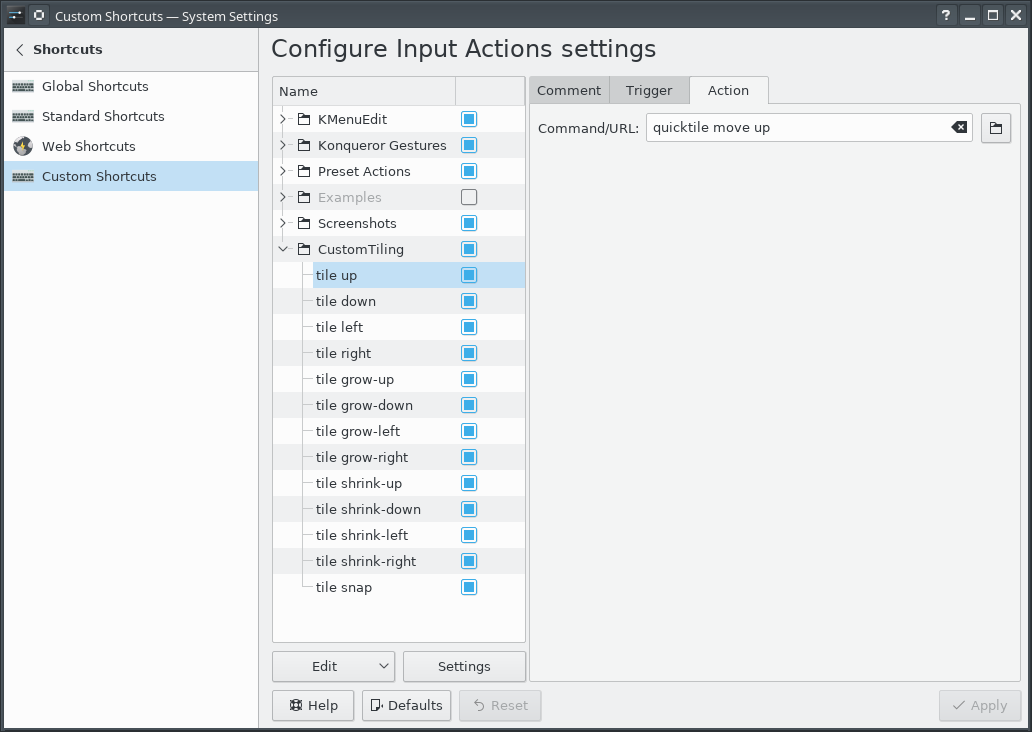
Grid-based Tiling Window Management, Mark III, aka QuickGridZones
With a laptop and a 4K monitor, I wind up with a large number of windows scattered across my screens. The general disarray of scattered and randomly offset windows drives me nuts.
I've done some work to address this problem before (here and here), which I had been referring to as "quicktile". But that's what KDE called its implementation that allowed snapping the window to either half of the screen, or to some quarter. On Windows, there's a Power Tool called "Fancy Zones" that also has a few similarities. In an effort to disambiguate what I've built, I've renamed my approach to "Quick Grid Zones".
Since the last post on this, I've done some cleanup of the logic and also ported it to work on Windows.
This isn't a cross-platform implementation, but rather three implementations with some structural similarities, implemented on top of platform-specific tools.
- Linux KDE - KDE global shortcuts that call a Python script using xdotool, wmctrl, and xprop
- Mac OS - a lua script for Hammerspoon
- Windows - an AutoHotKey2 script
Simple demo of running this on KDE:
Grab the local tarball for this release, or check out the QuickGridZones project page.
Grid-based Tiling Window Management, Mark II
A few years ago, I implemented a grid-based tiling window management tool for Linux/KDE that drastically improved my ability to utilize screen realestate on a 4K monitor.
The basic idea is that a 4K screen is divided into 16 cells in a 4x4 grid, and a Full HD screen is divided into 4 cells in a 2x2 grid. Windows can be snapped (Meta-Enter) to the nearest rectangle that aligns with that grid, whether that rectangle is 1 cell by 1 cell, or if it is 2 cells by 3 cells, etc. They can be moved around the grid with the keyboard (Meta-Up, Meta-Down, Meta-Left, Meta-Right). They can be grown by increments of the cell size in the four directions (Ctrl-Meta-Up, Ctrl-Meta-Down, Ctrl-Meta-Left, Ctrl-Meta-Right), and can be shrunk similarly (Shift-Meta-Up, Shift-Meta-Down, Shift-Meta-Left, Shift-Meta-Right).
While simple in concept, it dramatically improves the manageability of a large number of windows on multiple screens.
Since that first implementation, KDE or X11 introduced a change that broke some of the logic in the quicktile code for dealing with differences in behavior between different windows. All windows report location and size information for the part of the window inside the frame. When moving a window, some windows move the window inside the frame to the given coordinates (meaning that you set the window position to 100,100, and then query the location and it reports as 100,100). But other windows move the window _frame_ to the given coordinates (meaning that you set the window position to 100,100, and then query the location and it reports as 104,135). It used to be that we could differentiate those two types of windows because one type would show a client of N/A, and the other type would show a client of the hostname. But now, all windows show a client of the hostname, so I don't have a way to differentiate them.
Fortunately, all windows report their coordinates in the same way, so we can set the window's coordinates to the desired value, get the new coordinates, and if they aren't what were expected, adjust the coordinates we request by the error amount, and try again. That gets the window to the desired location reliably.
The downside is that you do see the window move to the wrong place and then shift to the right place. Fixing that would require finding some characteristic that can differentiate between the two types of windows. It does seem to be consistent in terms of what program the window is for, and might be a GTK vs QT difference or something. Alternatively, tracking the error correction required for each window could improve behavior by making a proactive adjustment after the first move of a window. But that requires maintaining state from one call of quicktile to the next, which would entail saving information to disk (and then managing the life-cycle of that data), or keeping it in memory using a daemon (and managing said daemon). For the moment, I don't see the benefit being worth that level of effort.
Here is the updated quicktile script.
To use the tool, you need to set up global keyboard shortcuts for the various quicktile subcommands. To make that easier, I created an importable quicktile shortcuts config file for KDE.
Of late I have also noticed that some windows may get rearranged when my laptop has the external monitor connected or disconnected. When that happens, I frequently wind up with a large number of windows with odd shapes and in odd locations. Clicking on each window, hitting Meta-Enter to snap it to the grid, and then moving it out of the way of the next window gets old very quickly. To more easily get back to some sane starting point, I added a quicktile snap all subcommand which will snap all windows on the current desktop to the grid. The shortcuts config file provided above ties that action to Ctrl-Meta-Enter.
This version works on Fedora 34; I have not tested on other distributions.
Filtering embedded timestamps from PNGs
PNG files created by ImageMagick include an embedded timestamp. When programatically generating images, sometimes an embedded timestamp is undesirable. If you want to ensure that your input data always generates the exact same output data, bit-for-bit, embedded timestamps break what you're doing. Cryptographic signature schemes, or content-addressible storage mechanisms do not allow for even small changes to file content without changing their signature or address. Or if you are regenerating files from some source and tracking changes in the generated files, updated timestamps just add noise.
The PNG format has an 8-byte header followed by chunks with a length, type, content, and checksum. The embedded timestamp chunk has a type of tIME. For images created directly by ImageMagick, there are also creation and modification timestamps in tEXt chunks.
To see this for yourself:
convert -size 1x1 xc:white white-pixel-1.png
sleep 1
convert -size 1x1 xc:white white-pixel-2.png
cmp -l white-pixel-{1,2}.png
That will generate two 258-byte PNG files, and show the differences between the binaries. You should see output something like this:
122 3 4 123 374 142 124 52 116 125 112 337 126 123 360 187 63 64 194 156 253 195 261 26 196 32 44 197 30 226 236 63 64 243 37 332 244 354 113 245 242 234 246 244 52
I have a project where I want to avoid these types of changes in PNG files generated from processed inputs. We can remove these differences from the binaries by iterating over the chunks and dropping those with a type of either tIME or tEXt. So I wrote a bit of (Python 3) code (png_chunk_filter.py) that allows filtering specific chunk types from PNG files without making any other modifications to them.
./png_chunk_filter.py --verbose --exclude tIME --exclude tEXt \
white-pixel-1.png white-pixel-1-cleaned.png
./png_chunk_filter.py --verbose --exclude tIME --exclude tEXt \
white-pixel-2.png white-pixel-2-cleaned.png
cmp -l white-pixel-{1,2}-cleaned.png
Because of the --verbose option, you should see this output:
Excluding tEXt, tIME chunks Found IHDR chunk Found gAMA chunk Found cHRM chunk Found bKGD chunk Found tIME chunk Excluding tIME chunk Found IDAT chunk Found tEXt chunk Excluding tEXt chunk Found tEXt chunk Excluding tEXt chunk Found IEND chunk Excluding tEXt, tIME chunks Found IHDR chunk Found gAMA chunk Found cHRM chunk Found bKGD chunk Found tIME chunk Excluding tIME chunk Found IDAT chunk Found tEXt chunk Excluding tEXt chunk Found tEXt chunk Excluding tEXt chunk Found IEND chunk
The cleaned PNG files are each 141 bytes, and both are identical.
usage: png_chunk_filter.py [-h] [--exclude EXCLUDE] [--verbose] filename target Filter chunks from a PNG file. positional arguments: filename target optional arguments: -h, --help show this help message and exit --exclude EXCLUDE chunk types to remove from the PNG image. --verbose list chunks encountered and exclusions
The code also accepts - in place of the filenames to read from stdin and/or write to stdout so that it can be used in a shell pipeline.
Another use for this code is stripping every unnecessary byte from a png to acheive a minimum size.
./png_chunk_filter.py --verbose \
--exclude gAMA \
--exclude cHRM \
--exclude bKGD \
--exclude tIME \
--exclude tEXt \
white-pixel-1.png minimal.png
That strips our 258-byte PNG down to a still-valid 67-byte PNG file.
Filtering of PNG files solved a problem I faced; perhaps it will help you at some point as well.
Grid-based Tiling Window Management
Many years ago, a coworker of mine showed me Window's "quick tiling" feature, where you would press Window-LeftArrow or Window-RightArrow to snap the current window to the left or right half of the screen. I then found that KDE on Linux had that same feature and the ability to snap to the upper-left, lower-left, upper-right, or lower-right quarter of the screen. I assigned those actions to the Meta-Home, Meta-End, Meta-PgUp, and Meta-PgDn shortcuts. (I'm going to use "Meta" as a generic term to mean the modifier key that on Windows machines has a Windows logo, on Linux machines has a Ubuntu or Tux logo, and Macs call "command".) Being able to arrange windows on screen quickly and neatly with keyboard shortcuts worked extremely well and quickly became a capability central to how I work.
Then I bought a 4K monitor.
With a 4K monitor, I could still arrange windows in the same way, but now I had 4 times the number of pixels. There was room on the screen to have a lot more windows that I could see at the same time and remain readable. I wanted a 4x4 grid on the screen, with the ability to move windows around on that grid, but also to resize windows to use multiple cells within that grid.
Further complicating matters is the fact that I use that 4K monitor along with the laptop's !FullHD screen which is 1920x1080. Dividing that screen into a 4x4 grid would be awkward; I wanted to retain a 2x2 grid for that screen, and keep a consistent mechanism for moving windows around on that screen and across screens.
KDE (Linux)
Unfortunately, KDE does not have features to support such a setup. So I went looking for a programatic way to control window size and placement on KDE/X11. I found three commandline tools that among them offered primitives I could build upon: xdotool, wmctrl, and xprop.
My solution was to write a Python program which took two arguments: a command and a direction.
The commands were 'move', 'grow', and 'shrink', and the directions 'left', 'right', 'up', and 'down'. And one additional command 'snap' with the location 'here' to snap the window to the nearest matching grid cells. The program would identify the currently active window, determine which grid cell was a best match for the action, and execute the appropriate xdotool commands. Then I associated keyboard shortcuts with those commands. Meta-Arrow keys for moving, Meta-Ctrl-Arrow keys to grow the window by a cell in the given direction, Meta-Shift-Arrow to shrink the window by a cell from the given direction, and Meta-Enter to snap to the closest cell.
Conceptually, that's not all that complicated to implement, but in practice:
Window geometry has to be adjusted for window decorations. But there appears to be a bug with setting the position of a window. The window coordinates used by the underlying tools for setting and getting the geometries do not include the frame, except for setting the position of the window, on windows that have a 'client' of the machine name instead of N/A. Getting the position, getting the size, and setting the size, all use the non-frame values. Windows with a client of N/A use the non-frame values for everything. A border width by title bar height offset error for only some of the windows proved to be a vexing bug to track down.
The space on a secondary monitor where the taskbar would be is also special, even if there is no task bar on that monitor; attempting to move a window into that space causes the window to shift up out of that space, so there remains an unused border on the bottom of the screen. Annoying, but I have found no alternative.
Move operations are not instantaneous, so setting a location and immediately querying it will yield the old coordinates for a short period.
A window which is maximized does not respond to the resize and move commands (and attempting it will cause xdotool to hang for 15 seconds), so that has to be detected and unmaximized.
A window which has been "Quick Tiled" using KDE's native quick-tiling feature acts like a maximized window, but does not set the maximized vert or maximized horz state flags, so cannot be detected with xprop, and to get it out of the KDE quick tiled state, it must be maximized and then unmaximized. So attempting to move a KDE quick tiled window leads to a 15 second pause, then the window maximizing briefly, and then resizing to the desired size. In practice, this is not much of an issue since my tool has completely replaced my use of KDE's quick-tiling.
OS X
I recently whined to a friend about not having the same window management setup on OS X; and he pointed me in the direction of a rather intriguing open source tool called Hammerspoon which lets you write Lua code to automate tasks in OS X and can assign keyboard shortcuts to those actions. That has a grid module that offers the necessary primitives to accomplish the same goal.
After installing Hammerspoon, launching it, and enabling Accessibility for Hammerspoon (so that the OS will let it control application windows), use init.lua as your ~/.hammerspoon/init.lua and reload the Hammerspoon config. This will set up the same set of keyboard shortcuts for moving application windows around as described in the KDE (Linux) section. For those who use OS X as their primary system, that set of shortcuts are going to conflict with (and therefore override) many of the standard keyboard shortcuts. Changing the keyboard shortcuts to add the Option key as part of the set of modifiers for all of the shortcuts should avoid those collisions at the cost of either needing another finger in the chord or putting a finger between the Option and Command keys to hit them together with one finger.
I was pleasantly surprised with how easily I could implement this approach using Hammerspoon.
Demo
Simple demo of running this on KDE:
(And that beautiful background is a high resolution photo by a friend and colleague, Sai Rupanagudi.)
Subtleties of colorizing unified diff output
I wanted to colorize unified diff output on the commandline; red for deletions and green for additions. As I learned on StackOverflow, there is colordiff which is the right solution for the problem. But why use an existing solution written by someone else in 400 lines of Perl, when you can use a partial solution of your own in one line of sed?
Wait... don't answer that.
So here's a one-liner that highlights deletions with a red background and additions with a green background, and hunk markers in blue text.
sed 's/^-/\x1b[41m-/;s/^+/\x1b[42m+/;s/^@/\x1b[34m@/;s/$/\x1b[0m/'
I chose to highlight changes using a background color so that whitespace changes would be more readily apparent. Interestingly, xterm does not display a background color for tab characters. This means that you are able to clearly see tab <-> space indentation changes in a diff. However, it also means that you can't see changes of trailing tabs. Sadly, colordiff does not support background colors.
Filenames are highlighted in the same way as content... for a good reason. You see, to differentiate between a filename line and a content line, you have to fully parse the diff output. Otherwise, if you add a line of text to a file that looks like:
++ vim73/src/ui.c 2013-06-01 14:48:45.012467754 -0500
you will get a line in your unified diff that looks like:
+++ vim73/src/ui.c 2013-06-01 14:48:45.012467754 -0500
which any regex-based approach is going to incorrectly see as a diff filename header. Clearly the same problem arises when deleting lines that start with --. Since colordiff is also a line-by-line regex-based implementation, it also highlights filenames the same as content. This is one of those cases where you can change your problem specification to make your solution trivial.
Example:
- evil.orig
blah blah blah humbug one two three four five six -- vim73/src/ui.c 2013-06-01 14:48:45.012467754 -0500 @@ -1,6 +1,6 @@ blah blah blah one two three four five six eight nine ten zero humbug
- evil.new
blah blah blah bah humbug one two three four five six ++ vim73/src/ui.c 2013-06-01 14:48:45.012467754 -0500 @@ -1,6 +1,6 @@ blah blah blah one two three four five six seven eight nine ten zero humbug
Yields a misleading unified diff that looks like:
--- evil.orig 2013-06-01 16:18:25.282693446 -0500 +++ evil.new 2013-06-01 16:30:27.535803954 -0500 @@ -1,12 +1,12 @@ blah blah blah -humbug +bah humbug one two three four five six --- vim73/src/ui.c 2013-06-01 14:48:45.012467754 -0500 +++ vim73/src/ui.c 2013-06-01 14:48:45.012467754 -0500 @@ -1,6 +1,6 @@ blah blah blah one two three four five six -eight nine ten +seven eight nine ten zero humbug
That one space before the false hunk header is probably the most visually apparent clue that something isn't right. Unless you're paying attention to the actual numbers in the hunk header, that is; but if the hunk is a couple hundred lines long and the false diff portion is only a couple of lines, even that would be hard to notice.
Colorize the diff (with my sed implementation),
--- evil.orig 2013-06-01 16:18:25.282693446 -0500 +++ evil.new 2013-06-01 16:30:27.535803954 -0500 @@ -1,12 +1,12 @@ blah blah blah -humbug +bah humbug one two three four five six --- vim73/src/ui.c 2013-06-01 14:48:45.012467754 -0500 +++ vim73/src/ui.c 2013-06-01 14:48:45.012467754 -0500 @@ -1,6 +1,6 @@ blah blah blah one two three four five six -eight nine ten +seven eight nine ten zero humbug
... and it is slightly less subtle.
Perhaps there is a case here for a diff colorizer built on a real parse of a unified diff?
On Variable-length Integer Encoding
Suppose you want to represent data in a serialized form with the length prepended to the data. You can do something like what Pascal does with strings, and prefix it with an 8-bit length. But that only gives you 0 through 255 bytes of data. So you need something larger, such as a 64-bit value. But then a single-byte data value takes up 9 bytes including the length indicator. We'd really want small data values to use a small amount of overhead to encode the length, and we'd want the large data values to be representable, too. And thus, we want a variable-length encoding of the length. And the length is an integer, so we want a variable-length encoding of an integer. We'll start with representing a non-negative value, but a variable-length encoding of a signed integer may be worth a look too.
You can find some interesting articles on wikipedia about universal codes which are variable-length encodings of integers, but they focus on representations of integers in bit-streams. Given our usecase, we're really dealing with byte-streams.
So let's start with a simple idea: Count the number of leading 1 bits and call that N. The total size of the numeric representation is 2N bytes. Take those bytes, mask off the N leading 1 bits, and interpret the number as a binary integer.
Let's try that:
0b00000000 = 0
0b00000001 = 1
:
0b01111111 = 127
0b10000000 00000000 = 0
0b10000000 00000001 = 1
:
0b10111111 11111111 = 16383
That gives us a way to represent any non-negative integer value. But there is one undesirable characteristic of this approach: there are multiple correct ways to represent any given number. For instance, the number 0 can be represented in a single byte as 0b00000000 or in two bytes as 0b10000000 00000000. This introduces ambiguity when encoding the value 0. There may be situations where this is a desirable property, but in this case, I want there to be one and only one representation of each integer.
A simple solution is to make the representations not overlap by adding the number of valid shorter representations to the integer representation. That is, interpret the 2-byte value as an integer, then add the number of valid 1-byte values to it, And for the 4-byte value, add the number of valid 2-byte and 1-byte values to it. An alternative way to state this is to add the largest number you can represent in the 2(N-1)-byte representation (plus one) to the integer.
That gives us:
0b00000000 = 0
0b00000001 = 1
:
0b01111111 = 127
0b10000000 00000000 = 128
0b10000000 00000001 = 129
:
0b10111111 11111111 = 16511
0b11000000 00000000 00000000 00000000 = 16512
0b11000000 00000000 00000000 00000001 = 16513
:
0b11011111 11111111 11111111 11111111 = 536887423
Here is a simplistic Python implementation. One of the nice things about using Python is that it can natively handle huge integers, so only the serialization aspect is needed.
This approach can be generalized in a couple of ways.
The first is that this could be done using leading 0 bits instead of leading 1 bits. I prefer the leading 1 bits because the 1-byte values 0-127 are the same as your normal unsigned char. But whether it is defined as the number of leading 1-bits or 0-bits, it still gives us a way to determine the value of N.
The second is in the translation of N into a representation size in bytes. I chose 2N, but it could just as easily be any function of N. If you wanted to have the size of the representation grow more slowly, you could use f(N) = N + 1. I like f(N) = 2N in part because it gives 1-byte, 2-byte, 4-byte, 8-byte representations that fit well into the natural integer sizes on modern computers.
This can also be generalized to signed integers as long as you define a mapping from the set of non-negative integers to the set of integers. A trivial solution would be to take the least significant bit to be a sign bit, though this gives you a way to represent negative zero. I suppose you could use that as a representation of Not-a-Number (NaN) or something along those lines. Alternatively, use a two's complement representation, though care would have to be taken with sign-extending the value and adding to that the largest magnitude negative or positive value that would overflow the next-smaller representation. This is left as an exercise to the reader.
Returning to our original problem statement, we now have a way to prepend a length to a data value while having the overhead cost low for small values while still supporting very large values. One byte of overhead to represent the length for data of 0 through 127 bytes is acceptable. Two bytes for 128 through 16511 bytes is also fine. By the time the overhead reaches 8 bytes, you're dealing with half a gigabyte of data.
But such a representation has additional possible uses. One that I have toyed with is using such a representation for a binary network communication protocol. Each message you define gets assigned an integer value, and you don't have to commit to a specific maximum number of message types when you define your protocol. Were I to use this for a protocol, I would want to make a 'version check' message have a numeric value < 128 so it fits in a single byte. And most messages would get a number that would map to a 2-byte value. That way, as messages are determined to be bandwidth "hot spots", they can be moved to a <128 value to cut a byte off their representation. The other thing I would probably do with protocol numbers would be to define a different f(N) that would grow the size of the integer representation more slowly. For that matter, it would be possible to map f(0) -> 1, f(1)->2, f(2)->2, f(3)->2, f(4)->3, etc; this would complicate some of the math, but would allow packing more values into 2 bytes. (The number of values represented by the second and third 2-byte representations would be half or a quarter of what the first 2-byte representation supported.) In a case like this, I would probably only define f(N) for the values of N I actually expect to use, and extend the definition as need arose.
Network protocols is another case where the unique nature of the representation is important. When you are dealing with systems that you want to secure (such as a network protocol), you do not want the ambiguity in the encoding process that a non-unique encoding implies. You want one and only one representation of each possible value so any attacker has no flexibility in doing something strange like using 256 bytes to represent the number 0.
I was prompted to post this by a question on programmers.stackexchange.com.
 rss
rss